Converting an Equation of a Circle from General to Standard Form
(KS3, Year 8)

We can convert an equation of a circle from general form to standard form.
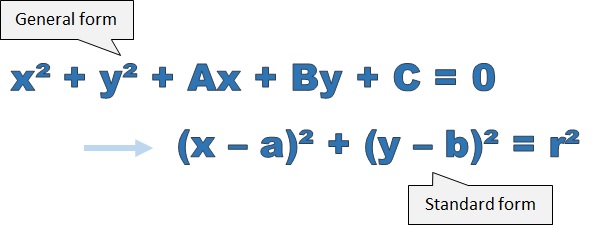
Why Convert from General Form to Standard Form?
- In general form, A, B and C do not tell us anything about the circle.

In standard form, • a and b tells us that (a, b) are the Cartesian coordinates of the center of the circle. • r tells us the radius of the circle.  If we are given a circle in general form, we can convert it to standard form to understand more about the circle.
If we are given a circle in general form, we can convert it to standard form to understand more about the circle.
A Real Example of How to Convert an Equation of a Circle from General to Standard Form
Question

Convert the equation of a circle in general form shown below into standard form. Find the center and radius of the circle.
Step-by-Step:
1
Group the x's and y's together.

2
Consider the x 2 and x terms only.

3

Write an x in the brackets.

Look at the original equation. Find the sign in front of the x term. In our example, it is −. Write this sign after the x in the brackets.

We have completed the square on these terms.

4
Consider the y 2 and y terms only.

5

Write a y in the brackets.

Look at the original equation. Find the sign in front of the y term. In our example, it is −. Write this sign after the y in the brackets.

Look at the original equation. Find the number in front of the y term (called the coefficient of y). In our example, it is 4.

Divide the coefficient of y by 2.
 step 5 5" width="521" height="119" />
step 5 5" width="521" height="119" />
We have completed the square on these terms.

6
Add the numbers outside of the brackets together.

− 1 + − 4 + − 4 = − 1 − 4 − 4 = − 9

7
Rearrange the equation so the number is on the right hand side of the equals sign (=).
| (x − 1) 2 + (y − 2) 2 − 9 = 0 |
| (x − 1) 2 + (y − 2) 2 − 9 + 9= 0 + 9 | Add 9 to boths sides |
| (x − 1) 2 + (y − 2) 2 = 9 |
Answer:
We have converted x 2 + y 2 − 2x − 4y − 4 = 0 (in general form) to (x − 1) 2 + (y − 2) 2 = 9 (in standard form). This is a circle centred at (1, 2) with a radius of 9.

how to find the centre and radius from the equation of a centre
Lesson Slides
The slider below gives a real example of how to convert an equation of a circle from general form to standard form.
This page was written by Stephen Clarke.

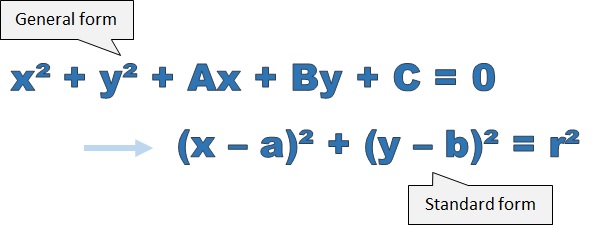
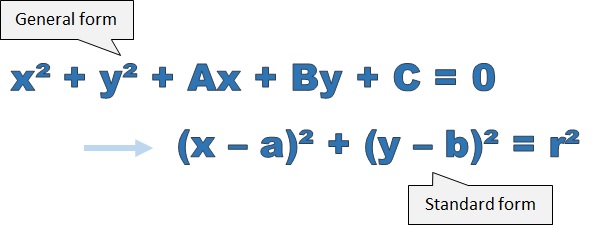



![]()
![]()
![]()
![]()

![]()


![]()
![]()
![]()
![]()

![]()
 step 5 5" width="521" height="119" />
step 5 5" width="521" height="119" />
![]()
![]()
![]()
